In quantum computing, gates are represented by unitary matrices. Unitary matrices are special matrices that, when multiplied by their conjugate transpose (also known as the adjoint or Hermitian conjugate), result in the identity matrix. The unitarity property ensures that the evolution of a quantum system under the action of these gates preserves the normalization of quantum states.
Overview of how the Gate Matrix is shown here:
Pauli-X Gate (NOT Gate)
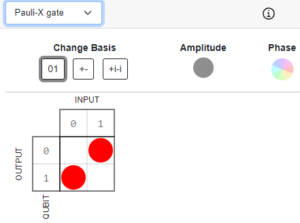
The Pauli-X gate is represented by the following matrix: X=[0110]
Pauli-Y Gate
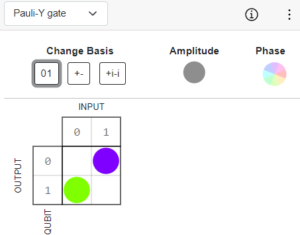
The Pauli-Y gate is represented by the following matrix: Y=[0−i0]
Pauli-Z Gate
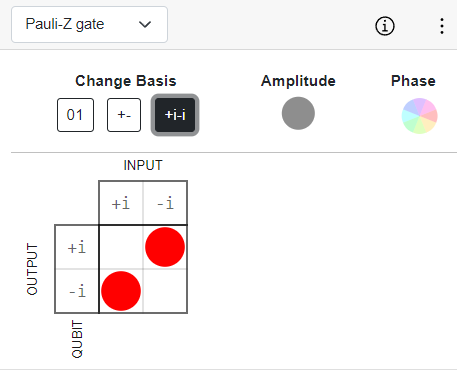
The Pauli-Z gate is represented by the following matrix: Z=[100−1]
Hadamard Gate
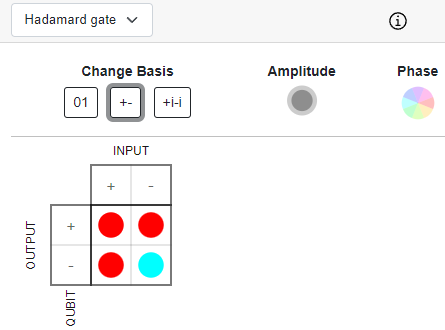
The Hadamard gate is represented by the following matrix: H=12[111−1]
Identity Gate
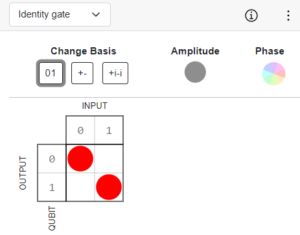
In quantum computing, the identity gate matrix is represented by the identity matrix, I. This gate leaves the state vector unchanged when applied to it. It essentially does nothing and is represented by a square with the letter “I” in a circuit diagram.
Phase(S) Gate
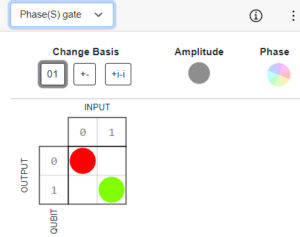
The S gate, also known as the phase gate or the Z90 gate, is a single-qubit operation that rotates a qubit by 90 degrees around the z-axis. The matrix representation of the S gate is [1 0; 0 exp(iπ/2)], which is equivalent to [1 0; 0 i].
Phase(T) Gate
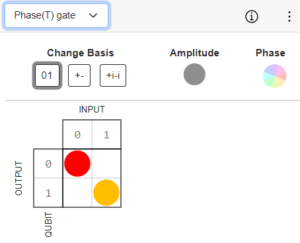
The T gate is a phase gate that rotates a qubit’s state by 45 degrees around the Z-axis of the Bloch sphere. It is also referred to as the π/4 gate because it rotates the qubit state by π/4 radians. The T gate is a non-Clifford gate that operates on a single qubit, taking one bit as input and returning one bit as output.