In quantum computing, operations on qubits are performed using quantum gates, which are mathematically represented by unitary matrices. A key characteristic of these gate matrices is that they preserve the total probability of quantum states. This is guaranteed by their unitarity: when a gate’s matrix is multiplied by its conjugate transpose, the result is the identity matrix. This property ensures that applying a quantum gate doesn’t alter the overall ‘length’ of a quantum state vector, thus maintaining its valid probabilistic interpretation. However, when we measure a qubit after applying a gate, we observe a classical outcome. This measurement is performed in a chosen basis. While the most common basis is the computational basis (|0⟩ and |1⟩), we can also measure in other bases, such as the X, Y, or Z bases.
- Z Basis: This is the standard computational basis, with eigenstates |0⟩ and |1⟩.
- X Basis: Also known as the Hadamard basis, with eigenstates |+⟩ = (|0⟩ + |1⟩)/√2 and |-⟩ = (|0⟩ – |1⟩)/√2.
- Y Basis: With eigenstates |+i⟩ = (|0⟩ + i|1⟩)/√2 and |-i⟩ = (|0⟩ – i|1⟩)/√2.
The probabilities of observing each outcome in a given basis are determined by the squared magnitudes of the amplitudes of the quantum state in that basis. The unitary gates manipulate these amplitudes, influencing the probabilities of measurement outcomes in any chosen basis, while always ensuring that the sum of all probabilities must equal 1.
An overview of the Gate Matrix is presented here:
Pauli-X Gate (NOT Gate) #

The Pauli-X gate is represented by the following matrix: X=[0110]
Pauli-Y Gate #

The Pauli-Y gate is represented by the following matrix: Y=[[0,−i], [i,0]]
Pauli-Z Gate #
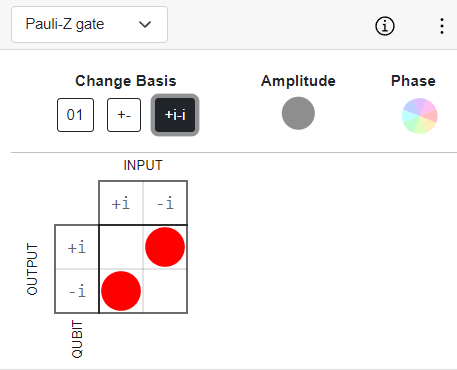
The Pauli-Z gate is represented by the following matrix: [[1,0], [0, -1]]
Hadamard Gate #
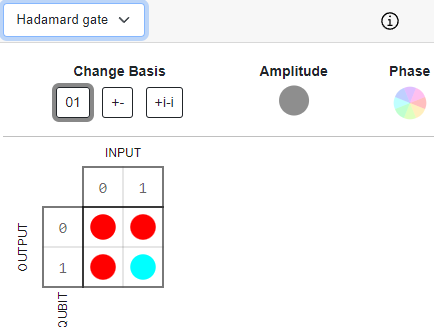
The Hadamard gate is represented by the following matrix: H = (X + Z)/\sqrt{2} = (1/\sqrt{2})*[[1,1],[1,-1]]
Identity Gate #

In quantum computing, the identity gate matrix is represented by the identity matrix, I. This gate leaves the state vector unchanged when applied to it. It essentially does nothing and is represented by a square with the letter “I” in a circuit diagram.
The Identity gate is represented by the following matrix : [[1,0],[0,1]]
Phase(S) Gate #

The S gate, also known as the phase gate or the Z90 gate, is a single-qubit operation that rotates a qubit by 90 degrees around the z-axis. The matrix representation of the S gate is [[1 0] [0 exp(iπ/2)]], which is equivalent to [[1,0],[0, i]].
Phase(T) Gate #

The T gate is a phase gate that rotates a qubit’s state by 45 degrees around the Z-axis of the Bloch sphere. It is also referred to as the π/4 gate because it rotates the qubit state by π/4 radians. The T gate is a non-Clifford gate that operates on a single qubit, taking one bit as input and returning one bit as output.
T gate matrix is represented as: T [[1,0],[0,e^{i \pi/4}]]